
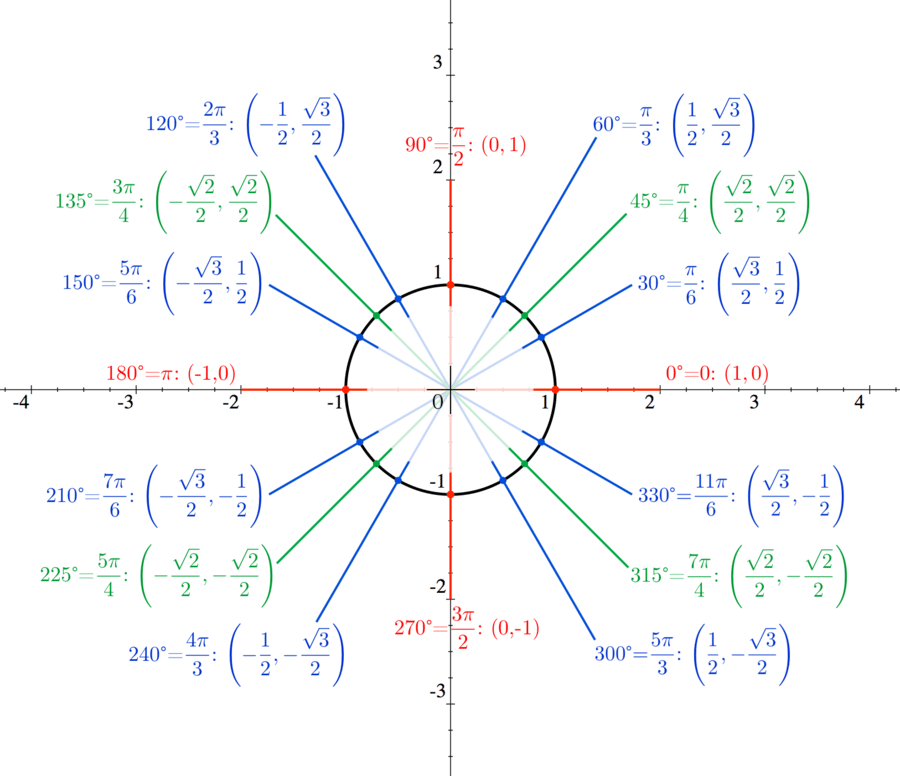
With information from one of these points, we can calculate the sine, cosine and tangent of the other three.Ĭalculate the angle for each point, and compare the, coordinates given on the diagram with and values given for the angle on your calculator. In the following applet a point in the first quadrant is reflected to make a total of four points. This handout will describe unit circle concepts, define degrees and radians.

The following diagram is a helpful for remembering which trig values are positive where.Ī simpler version of the diagram is often referred to as the CAST diagram:Ī reference angle is an angle in the first quadrant. The unit circle can be used to calculate the trigonometric functions sin(). We refer to the quadrants of the Cartesian Plane as follows: These are positive on one diagonal and negative on the other.

coordinates are positive in the upper half of the diagram. Sine, Cosine, Tangent The measurements of sin, cos, and tan become clear when you see them on a graph. Values of sine are defined as the coordinate of the point P. The unit circle is a circle centered on the origin with a unit radius, 1. These are positive on the right hand side of the diagram. Values of cosine are defined as the coordinates of the point P. This leads to a simpler diagram for the values of sine and cosine:Īpplet link Positive and Negative values of Sine, Cosine, Tangent Remembering that gives us all three ratios. Let be the angle between the positive axis and the radius, measured counter-clockwise. Draw a radius from the center to the point P. Let P be a point on the circumference of a circle with radius one unit and center at the origin. We can now define the values of cosine and sine to be the values of a point on the circumference of the unit circle. Notice that some trig values are positive and some are negative. The unit circle shown on the applet below allows us to explore trig values between zero and 360 degrees. However, values of sine, cosine and tangent are defined for angles between negative infinity and positive infinity. A unit circle is a circle on the Cartesian Plane that has a radius of 1 unit and is centered at the origin (0, 0). When solving right angled triangles with SOH CAH TOA, we considered values of sine, cosine and tangent between zero and 90 degrees only, as follows: Notes/Exercise: Grade 11 Trigonometry Unit circle


 0 kommentar(er)
0 kommentar(er)
